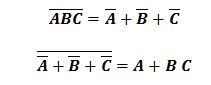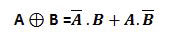Qu’appelle-t-on algèbre de BOOLE?
Un processeur est composé de plusieurs milliers de transistors permettant de réaliser des fonctions sur des signaux numériques .Ces transistors, assemblés entre eux forment des composants il est possible de créer des circuits réalisant des opérations très complexes .L’algèbre de Boole du nom mathématicien anglais : Georges Boole (1815-1864) est un moyen d’arriver à créer de tels circuits.
Les lois fondamentales de l’algèbre de BOOLE
Lois de commutativité :
a) A.B = B.A
b) A+B = B+A
Lois d’associativité :
a) (A.B).C = A. (B.C) = A. B. C
b) (A+B) +C = A +(B+C) = A+B+C
Lois de distribution :
a) A.(B+C) = (A.B)+(A.C)
b) A +(B.C) = (A+B).(A+C)
Lois d’idempotence :
a) A. A = A
b) A+A = A
Lois de complémentarité
Lois d’identité remarquable
a) 1. A = A
b) 1+A = 1
c) 0 .A = 0
d) 0 +A = A
Théorèmes de Morgan
OU Exclusif
Tableaux de Karnaugh
| AB/CD | 00 | 01 | 11 | 10 |
| 00 | 1 | 1 | 1 | 1 |
| 01 | 0 | 0 | 1 | 0 |
| 11 | 0 | 1 | 1 | 0 |
| 10 | 0 | 0 | 1 | 0 |
Le méthode de simplification de karnaugh repose sur l’identité
Elle est basée sur l’inspection visuelle de tableaux
disposés de façon telle que les cases adjacentes en ligne et en colonne
ne diffèrent que par l’état d’une variable et une seule.
Pour télécharge PDF cliquez ici
Pour télécharger les exercice PDF cliquez ici