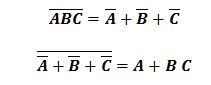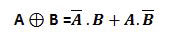Les exercices logique combinatoire parti 1 l'algèbre de BOOLE

Les exercices logique combinatoire parti 1 l'algèbre de BOOLE

        Exercice 1

        Soit la fonction logique « F2 » représentée par l’équation suivante :

a)      Dresser la table de vérité correspondante à la fonction logique « F2 »

b)      Simplifiez l’équation à l’aide des lois de l’algèbre de BOOLE

c)      Tracer le logigramme de la fonction « F2 »en utilisant les portes logiques « et »,

 « ou »et « non » à deux entrées.

Exercice 2

Soit la fonction logique « S2 » représentée par l’équation suivante :

a)      Dresser la table de vérité correspondante à la fonction logique « S2 »

b)      Simplifiez l’équation à l’aide des lois de l’algèbre de BOOLE

c)      Tracer le logigramme de la fonction « S2 »en utilisant les portes logiques « et », 

« ou »et « non » à deux entrées.

Exercice 3

Soit la fonction logique « S3 » représentée par l’équation suivante :

a)      Dresser la table de vérité correspondante à la fonction logique « S3 »

b)      Simplifiez l’équation à l’aide des lois de l’algèbre de BOOLE

c)      Tracer le logigramme de la fonction « S3 »en utilisant les portes logiques « et », 

« ou »et « non » à deux entrées.

Exercice 4

Soit la fonction logique « S4 » représentée par l’équation suivante :

d)      Dresser la table de vérité correspondante à la fonction logique « S4 »

e)      Simplifiez l’équation à l’aide des lois de l’algèbre de BOOLE

f)       Tracer le logigramme de la fonction « S4 »en utilisant les portes logiques « et », 

« ou »et « non » à deux entrées.

Exercice 5

Soit la fonction logique « S5 » représentée par l’équation suivante :

a)      Dresser la table de vérité correspondante à la fonction logique « S5 »

b)      Simplifiez l’équation à l’aide des lois de l’algèbre de BOOLE

c)      Tracer le logigramme de la fonction « S5 »en utilisant les portes logiques « et », 

« ou »et « non » à deux entrées.

Exercice 6

Refaite les Exercices 1-2-3-4-5

Simplifiez l’équation à l’aide du tableau de karnaugh

Exercice 7

Soit la fonction logique « S7 » représentée par l’équation suivante :

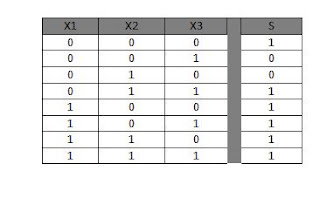
a)      Dresser la table de vérité correspondante à la fonction logique « S7»

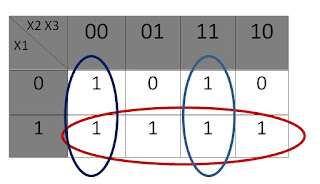
b)      Simplifiez l’équation à l’aide du tableau de karnaugh

c)      Tracer le logigramme de la fonction « S7 »en utilisant les portes logiques « et », 

« ou »et « non » à deux entrées.

Exercice 8

Soit la fonction logique « S8 » représentée par l’équation suivante :

a)      Dresser la table de vérité correspondante à la fonction logique « S8»

b)      Simplifiez l’équation à l’aide du tableau de karnaugh

c)      Tracer le logigramme de la fonction « S8 »en utilisant les portes logiques « et », 

« ou »et « non » à deux entrées.

Pour télécharger les exercices PDF cliquez ici

Pour télécharger solution les exercices PDF cliquez ici

أقراء المزيد

• شارك
• شارك

logique combinatoire Les lois fondamentales de l’algèbre de BOOLE

Qu’appelle-t-on algèbre de BOOLE? 

Un processeur est composé de plusieurs milliers de transistors permettant de réaliser des fonctions sur des signaux numériques .Ces transistors, assemblés entre eux forment des composants il est possible de créer des circuits réalisant des opérations très complexes .L’algèbre de Boole du nom mathématicien anglais : Georges Boole (1815-1864) est un moyen d’arriver à créer de tels circuits.

Les lois fondamentales de l’algèbre de BOOLE

Lois de commutativité :

a) A.B = B.A

b) A+B = B+A

Lois d’associativité :

a) (A.B).C = A. (B.C) = A. B. C

b) (A+B) +C = A +(B+C) = A+B+C

Lois de distribution :

a) A.(B+C) = (A.B)+(A.C)

b) A +(B.C) = (A+B).(A+C)

Lois d’idempotence :

a) A. A = A

b) A+A = A

Lois de complémentarité

Lois d’identité remarquable

a)      1. A = A

b)      1+A = 1

c)       0 .A = 0

d)      0 +A = A

Théorèmes de Morgan

OU Exclusif

Tableaux de Karnaugh

 

AB/CD	00	01	11	10
00	1	1	1	1
01	0	0	1	0
11	0	1	1	0
10	0	0	1	0

Le méthode de simplification de karnaugh repose sur l’identité

Elle est basée sur l’inspection visuelle de tableaux disposés de façon telle que les cases adjacentes en ligne et en colonne ne diffèrent que par l’état d’une variable et une seule.

Pour télécharge PDF cliquez ici

Pour télécharger les exercice  PDF cliquez ici

أقراء المزيد

• شارك
• شارك

Chair de Charge Logique Combinatoire

Chair de Charge Logique Combinatoire

Partie 1

On désire réaliser un circuit logique qui permet d’actionner une signalisation (Y) en fonction de l’état des variables (X1,X2,X3) suivant la situation suivante :

Y=1 pour les combinaisons suivantes de (X1,X2,X3) ; (000),(100),(011),(101),(111) et (110).

Y=0 pour les autres situations .

Travail demandé :

       1-Dresser la table de vérité de S.

    2-Trouver l’expression simplifiée de la fonction logique S en utilisant le tableau de Kharnaugh.

    3-Donner le schéma électrique de câblage pour réaliser la fonction simplifiée de S avec des portes
       NON ,ET et OU en utilisant les circuits (7408,7404,7432).

  Simuler la sortie par une LED.

     4-Monter le circuit logique sur plaquette d’essai et vérifier le fonctionnement.

   5-Donner le schéma électrique de câblage pour réaliser la fonction simplifiée de S avec des portes NON_ET en utilisant les circuits 7410.

Simuler la sortie par une LED.

     6- Monter le circuit logique sur plaquette d’essai et vérifier le fonctionnement.

Solution :

1-table de vérité de S

2- le tableau de Kharnaugh .

3-schéma électrique de câblage:

أقراء المزيد

• شارك
• شارك

How to make a digital clock with 7490 ic // ساعة رقمية 7490

How to make a digital clock with 7490 ic // ساعة رقمية 7490

clock 7490

دعونا نلقي نظرة على 7490 :

ic7490

7490 هو عداد العقد ، مما يعني أنه قادر على العد من 0 إلى 9 دوريًا ، وهذا هو الوضع الطبيعي. بمعنى أن QA و QB و QC و QD هي 4 بتات في رقم ثنائي ، وتدور هذه المسامير من 0 إلى 9 ، مثل هذا:

QD QC QB QA 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1

يمكنك أيضًا ضبط الشريحة لأعلى حتى يصل العدد الأقصى للأرقام الأخرى ثم العودة إلى الصفر. يمكنك "إعداده" عن طريق تغيير الأسلاك لخطوط R01 و R02 و R91 و R92. إذا كان كلا R01 و R02 1 (5 فولت) وإما R91 أو R92 تساوي 0 (أرض) ، فسوف تعيد الشريحة ضبط QA و QB و QC و QD إلى 0.

جميع المراحل تشاهدونها في هذا الفيديو:

لتحميل جميع الملفات من;

لتحميل برنامج PROTEUS من هنا.

أقراء المزيد

• شارك
• شارك